VIGAS EMPOTRADAS
Como ya hemos visto en los artículos anteriores dentro de éste capítulo a cerca de las vigas, que ellas son las responsables de las cargas de la estructura, y existen de madera, de hormigón, prefabricadas, etcétera, pero en este articulo, que a continuación presentamos, nos referiremos a las vigas empotradas, que como su palabra lo indica, se refiere a las vigas que además de apoyadas en ambos extremos, son las que se deben fijar con trabes para que no se muevan o se deslicen. Para empotrar ese tipo de vigas, se usan ciertos elementos de soporte, que pueden ser tornillos, o pernos tuercas, arandelas, y remaches de gran porte, y no uno solo sino seis o cuatro para cada caso en particular. Hay casos en los que este tipo de vigas se encuentran clavadas, de manera muy firme en una pared de extremo a extremo, pero apoyadas en otra viga que esa puede estar solo apoyada.Para colocar las vigas de una estructura se necesitan varios cálculos que quienes son los responsables de ellos son los ingenieros de la obra, es por ello que cada caso es único, y en donde se ponen este tipo de vigas, no se pueden colocar otros. Los ingenieros, mediante los cálculos y ecuaciones, llegan a la conclusión que los momentos de fuerzas son diferentes en cada caso, es por ello que en las estructuras se hacen necesario contar con ingenieros de obra que son quienes tienen la responsabilidad de hacer las correctas formulas y llevar a cabo los trabajos. Es muy simple la explicación, se trata de las vigas empotradas cuando se encuentran firmemente sujetadas mediante los anclajes correspondientes a otro medio de apoyo que en este caso es vertical, y que sirve de apoyo o sustento. Se hacen diagramas, planos, y estudios analizando cada detalle, ya que esas constituyen una parte fundamental en las estructuras.
Sí, por eso que en el caso de las vigas empotradas, podemos encontrar las bi empotradas o las semi apoyadas. Se necesitan vigas de gran porte para confeccionar las estructuras de una vivienda por ejemplo de madera, las que en la mayoría de los casos llevan las vigas empotradas, en la que se han llevado a cabo estudios de desplazamientos, y pendientes sobre las mismas, pero previos a la colocación y trabe. Estos son elementos estructurales, que van a recibir cargas en forma perpendicular y en posición horizontal, o muchas veces ligeramente inclinadas, y se pueden construir de un solo tramo, o de varios, eso es según el número de apoyos, los refuerzos se hacen en la cara superior y en la cara inferior de cada viga. En los casos en los que se necesiten estructuras más sólidas las vigas empotradas, deberán contar con otros elementos extras, para poder de esa manera aumentar la resistencia, y no la rigidez, por ejemplo para los casos en construcciones en zonas sísmicas.
I.- INTRODUCCIÓN
El análisis de las deformaciones en vigas nos permite limitar los descensos de las mismas, entregando secciones adecuadas y por otra parte incorporar nuevas expresiones para resolver vigas hiperestáticas.
Una forma de enfocar la resolución de las vigas hiperestáticas consiste en descomponer la viga inicial en varias vigas cuyo efecto sumado equivalga a la situación original.
Las solicitaciones externas, cargas y reacciones, generan cortante, momento y deformación, siendo válido el principio de descomposición de las vigas en vigas cuyas acciones sumen el mismo efecto.
Este principio puede ser aplicado a vigas hiperestáticas, tales como
- Vigas bi -empotradas
- Vigas empotrada-apoyada
- Vigas continuas
VIGA EMPOTRADA EN AMBOS EXTREMOS CON CARGA UNIFORMEMENTE REPARTIDA
En el caso de viga empotrada en sus dos extremos, la cantidad de reacciones desconocidas supera a la de ecuaciones que la estática dispone para el sistema. Para resolver las incógnitas es necesario disponer de otras ecuaciones basadas en las deformaciones.
Considerando que las pendientes de las tangentes trazadas en los dos extremos es nula, se plantean las siguientes ecuaciones
A= 0 B = 0
Para establecer las ecuaciones se descompone la viga dada en tres vigas supuestas que en conjunto equivalgan a la viga inicial.
a.- Viga simplemente apoyada con carga uniformemente repartida.
b.- Viga simplemente apoyada con momento aplicado en el extremo izquierdo (Ma).
c.- Viga simplemente apoyada con momento aplicado en el extremo derecho (Mb).
VIGA EMPOTRADA EN UN EXTREMO Y SIMPLEMENTE APOYADA EN EL OTRO, CON CARGA UNIFORMEMENTE DISTRIBUIDA.
En este caso de viga empotrada en uno de sus extremos, la cantidad de reacciones desconocidas también supera a la de ecuaciones de estática. Para resolver las incógnitas es necesario disponer de las ecuaciones basadas en las deformaciones.
Considerando que la pendiente de la tangente trazada en el extremo empotrado es nula, se plantea la ecuación:
A= 0
Se descompone la viga inicial en dos vigas supuestas que en conjunto equivalen a la viga inicial.
a.- Viga simplemente apoyada con carga uniformemente repartida.
b.- Viga simplemente apoyada con momento aplicado en el extremo izquierdo.
Vigas con soportes simples (biapoyadas)
Vigas en voladizo (ménsulas empotradas
Vigas Empotradas
Teoría de vigas de Euler-Bernoulli
La teoría de vigas es una parte de la resistencia de materiales que permite el cálculo de esfuerzos y deformaciones en vigas. Si bien las vigas reales sonsólidos deformables, en teoría de vigas se hacen ciertas simplificaciones gracias a las que se pueden calcular aproximadamente las tensiones, desplazamientos y esfuerzos en las vigas como si fueran elementos unidimensionales.
Los inicios de la teoría de vigas se remontan al siglo XVIII, trabajos que fueron iniciados por Leonhard Euler y Daniel Bernoulli. Para el estudio de vigas se considera un sistema de coordenadas en que el eje X es siempre tangente al eje baricéntrico de la viga, y los ejes Y y Z coincidan con los ejes principales de inercia. Los supuestos básicos de la teoría de vigas para la flexión simple de una viga que flecte en el plano XY son:
- Hipótesis de comportamiento elástico. El material de la viga es elástico lineal, con módulo de Young E y coeficiente de Poisson despreciable.
- Hipótesis de la flecha vertical. En cada punto el desplazamiento vertical solo depende de x: uy(x, y) = w(x).
- Hipótesis de la fibra neutra. Los puntos de la fibra neutra solo sufren desplazamiento vertical y giro: ux(x, 0) = 0.
- La tensión perpendicular a la fibra neutra se anula: σyy= 0.
- Hipótesis de Bernoulli. Las secciones planas inicialmente perpendiculares al eje de la viga, siguen siendo perpendiculares al eje de la viga una vez curvado.
Las hipótesis (1)-(4) juntas definen la teoría de vigas de Timoshenko. La teoría de Euler-Bernouilli es una simplificación de la teoría anterior, al aceptarse la última hipótesis como exacta (cuando en vigas reales es solo aproximadamente cierta). El conjunto de hipótesis (1)-(5) lleva a la siguiente hipótesis cinemática sobre los desplazamientos:
Deformaciones y tensiones en las vigas
Si se calculan las componentes del tensor de deformaciones a partir de estos desplazamientos se llega a:
A partir de estas deformaciones se pueden obtener las tensiones usando las ecuaciones de Lamé-Hooke, asumiendo  :
:
 :
:Esfuerzos internos en vigas
a partir de los resultados anteriores y de las ecuaciones de equivalencia pueden obtenerse sencillamente el esfuerzo normal, el esfuerzo cortante y el momento flector al que está sometida una sección de una viga sometida a flexión simple en la teoría de Euler-Bernouilli:
Ecuaciones de equilibrio
Las ecuaciones de equilibrio para una viga son la aplicación de las ecuaciones de la estática a un tramo de viga en equilibrio. Las fuerzas que intervienen sobre el tramo serían la carga exterior aplicada sobre la viga y las fuerzas cortantes actuantes sobre las secciones extremas que delimitan el tramo. Si el tramo está en equilibrio eso implica que la suma de fuerzas verticales debe ser cero, y además la suma de momentos de fuerza a la fibra neutra debe ser cero en la dirección tangente a la fibra neutra. Estas dos condiciones solo se pueden cumplir si la variación de esfuerzo cortante y momento flector están relacionada con la carga vertical por unidad de longitud mediante:
Cálculo de tensiones en viga
El cálculo de tensiones en vigas generalmente requiere conocer la variación de los esfuerzos internos y a partir de ellos aplicar la fórmula adecuada según la viga esté sometida a flexión, torsión, esfuerzo normal oesfuerzo cortante. El tensor tensión de una viga viene dado en función de los esfuerzos internos por:
Donde las tensiones pueden determinarse, aproximadamente, a partir de los esfuerzos internos. Si se considera un sistema de ejes principales de inercia sobre la viga, considerada como prisma mecánico, las tensiones asociadas a la extensión, flexión, cortante y torsión resultan ser:
Donde:
 son las tensiones sobre la sección transversal: tensión normal o perpendicular, y las tensiones tangenciales de torsión y cortante.
son las tensiones sobre la sección transversal: tensión normal o perpendicular, y las tensiones tangenciales de torsión y cortante. , son los esfuerzos internos: esfuerzo axial, momentos flectores y bimomento asociado a la torsión.
, son los esfuerzos internos: esfuerzo axial, momentos flectores y bimomento asociado a la torsión.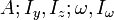 , son propiedades de la sección transversal de la viga: área, segundos momentos de área (o momentos de inercia), alabeo y momento de alabeo.
, son propiedades de la sección transversal de la viga: área, segundos momentos de área (o momentos de inercia), alabeo y momento de alabeo.
Las máximas tensiones normal y tangencial sobre una sección transversal cualquiera de la viga se pueden calcular a partir de la primera ( ) y tercera (
) y tercera ( ) tensión principal:
) tensión principal:
 ) y tercera (
) y tercera ( ) tensión principal:
) tensión principal:
En vigas metálicas frecuentemente se usa como criterio de fallo el que en algún punto la tensión equivalente de Von Mises supere una cierta tensión última definida a partir del límite elástico, en ese caso, el criterio de fallo se puede escribir como:










![[T]_{xyz} = \begin{bmatrix}
\sigma & \tau_{y} & \tau_{z} \\
\tau_{y} & 0 & 0 \\
\tau_{z} & 0 & 0
\end{bmatrix}](https://upload.wikimedia.org/math/6/7/2/6726ffdd0c1a05e10f3256802762d2b8.png)






 ) esté dentro de los límites admisibles;
) esté dentro de los límites admisibles;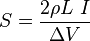
 la resistividad, la I la intensidad prevista en el conductor y
la resistividad, la I la intensidad prevista en el conductor y 
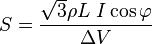
 es el factor de potencia activa.
es el factor de potencia activa. es la longitud del cable en metros.
es la longitud del cable en metros. .
.






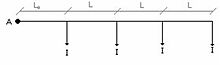


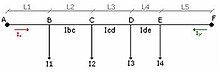
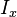 e
e 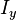 .
.




 )
)